The Art of Secure Communication: Exploring Diffie-Hellman Key Exchange
Diffie-Hellman is a key exchanging algorithm invented by Whitfield Diffie and Martin Hellman, that is used to generate a shared secret over an insecure channel. Diffie-Hellman key exchange plays a huge role in understanding concepts such as end-to-end encryption.
Before the invention of the Diffie-Hellman key exchange for two people say Alice and Bob to communicate securely with each other over a public or an insecure channel they'd have to share a key so when Alice encrypts a message and sends it to Bob, and Bob could use the key to decrypt the message and vice versa. Still, Alice can't simply send the key to Bob as anybody who's intercepting the traffic would be able to see the key, enabling them to decrypt the messages that Alice and Bob are sending each other.
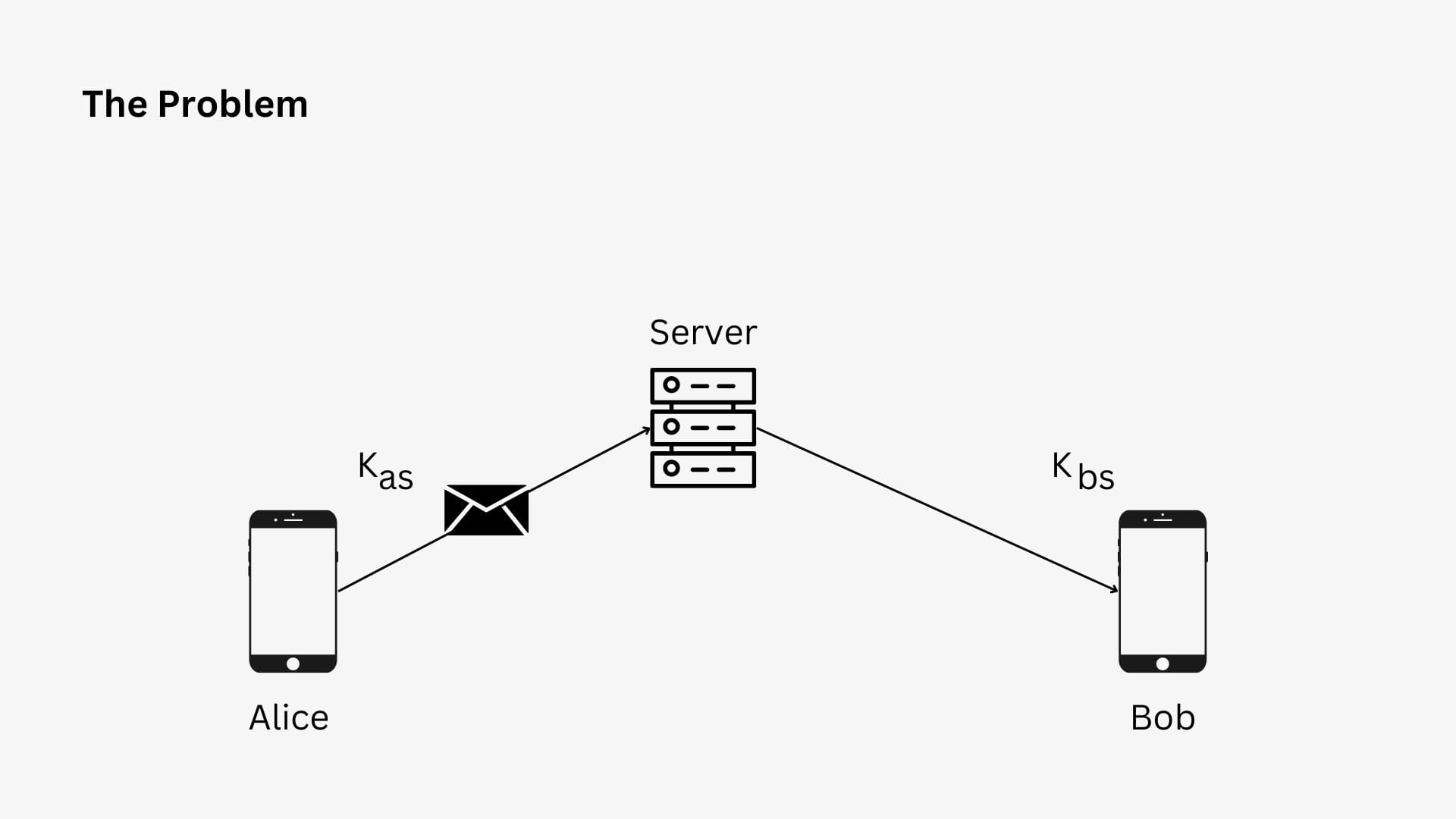
In most cases, messages would have to go through a centralized server before they reach the receiver's device in situations like this the server uses two different keys(Kas and Kbs), one for Alice and the other for Bob, Alice would encrypt the message using the key Kas and when the server received the message it would decrypt the message using Kas and again encrypt it using Bob's key(Kbs) and sends it to Bob upon receiving the message Bob would decrypt it using his key Kbs. The problem with this method is that there is a time when the messages are visible in plain text in the server that is, after the messages are decrypted using the key Kas and before they are again encrypted using the key Kbs, this would allow anyone with access to the server to read the messages exchanged between Alice and Bob.
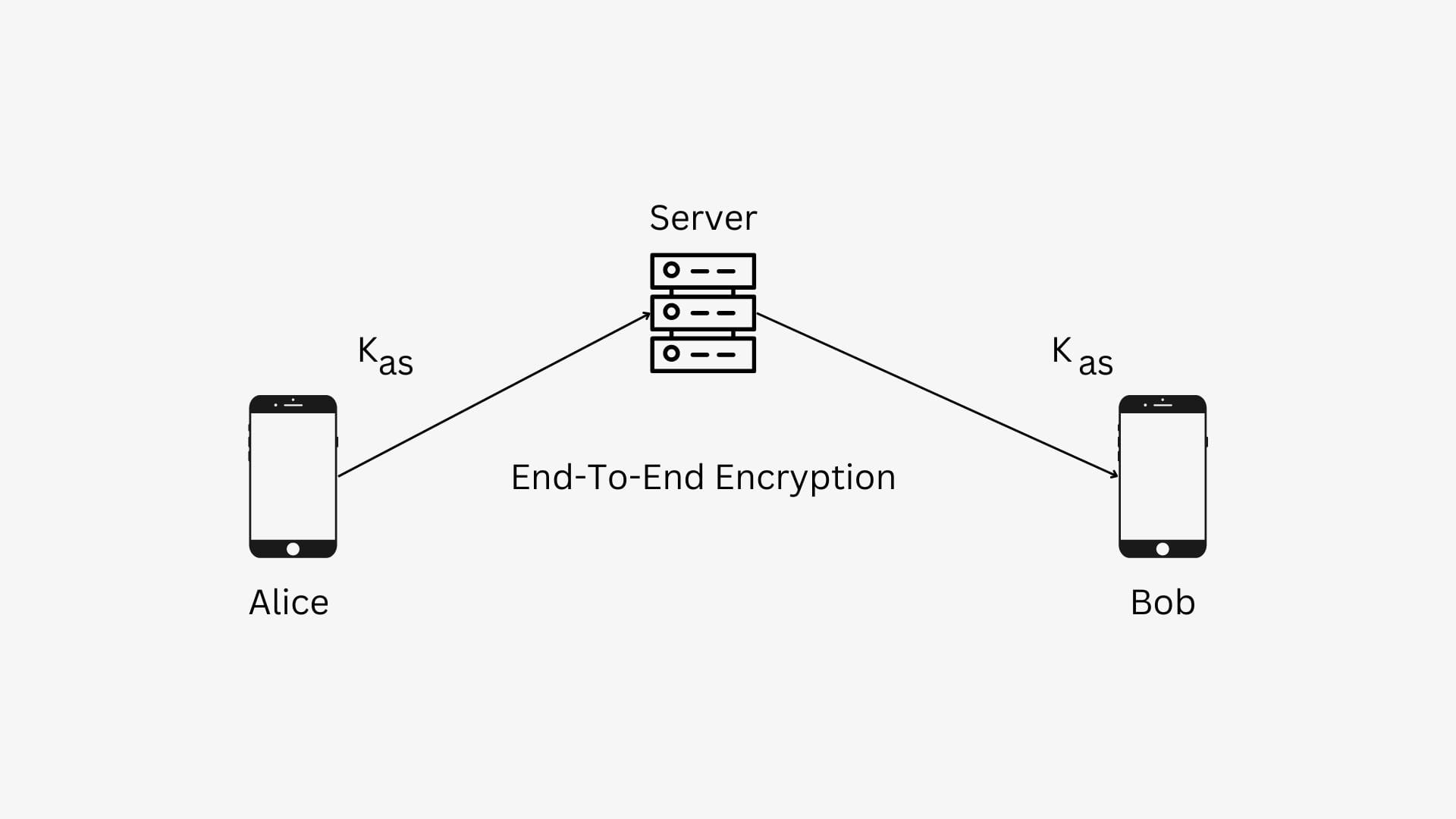
To solve this problem, Alice and Bob should use the shared key Kas, as discussed above, Alice cannot share her key with Bob, Diffie-Hellman solves this problem by generating the same key for Alice and Bob using two public variables and one private variable, public variables are the variables which are shared publicly that is anybody can view them, and the two variables which are not shared publicly are known as private variables.
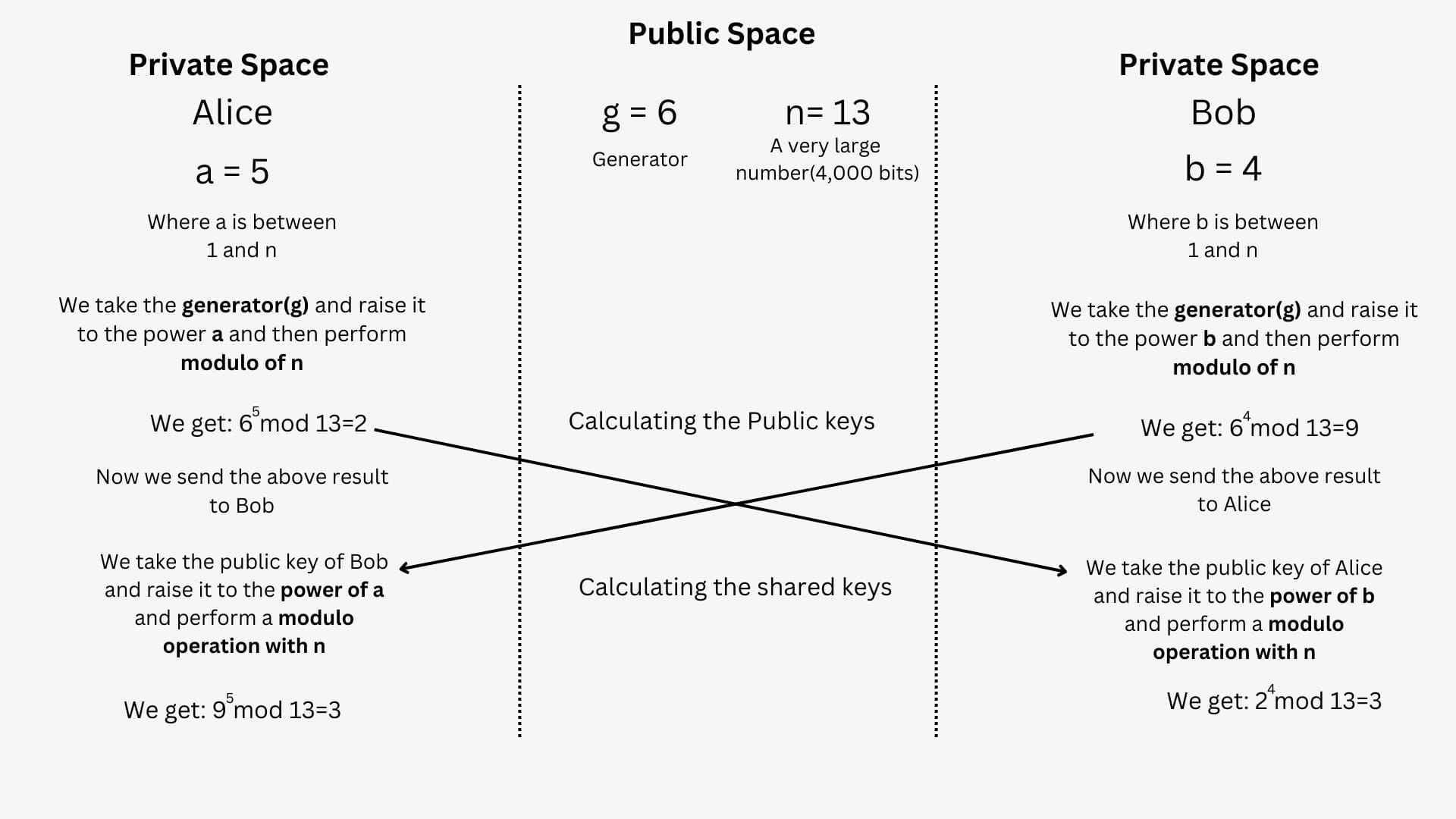
The two public variables are g and n where g is a small prime number also known as a "Generator" and n is a large 4,000-bit number. The private variables for Alice and Bob are a and b respectively where the values of a and b range from 1 to n, these values are not shared with anyone as they are private variables. The first step of the Diffie-Hellman key exchange is performing a Modular arithmetic operation to calculate the public keys. That is Alice takes the generator(g) raises to the power of a and performs a modulo operation with n when we substitute the values from the above example we'd get \(g^{a}\text{ } mod\text{ }n\) which is equal to \(6^{5}\text{ } mod\text{ }13=2\). Bob performs the same modular arithmetic operation on his side using his private variable b \(g^{a}\text{ } mod\text{ }n\) which is equal to \(6^{4}\text{ } mod\text{ }13=9\). Alice and Bob then exchange their public keys with each other, these can be shared publicly as the attacker would only know the values of g, n and the result from the modular arithmetic (2 in Alice's case) and finding the private value of Alice(a) using this information is considered very difficult as the attacker would have to solve the Discrete logarithm problem.
The second and last step of the Diffie-Helman key exchange is to calculate the shared secret using the exchanged public keys, that is Alice takes the public key of Bob raises it to the power of a and performs a modulo operation with n, and Bob would repeat the same step where he raises Alice's public to the power of b and performs a modulo operation with n resulting in the following output \[\text{For Alice}\Rightarrow9^{5}\text{ } mod\text{ }13=3\] \[\text{For Bob}\Rightarrow2^{4}\text{ } mod\text{ }13=3\]
As we can see both Alice and Bob now have the same shared key even though they started with completely different values and without the necessity to share or exchange any private keys. This shared secret or key is not used as is for the encryption instead it is used as a seed value in encryption algorithms such as AES(Advanced Encryption Standard). The security of the Diffie-Hellman depends on solving the Discrete logarithm problem which is very time-consuming as a result an attacker would have to resort to techniques such as brute-forcing, however with modern GPUs and computers faster and faster by the day, solving the Diffie-Hellman problem may become feasible in just a few years. This is largely due to the development of new algorithms, such as Elliptic Curve Cryptography (ECC).




